30 – funzioni ricorsive

Le funzioni che richiamano altre è una tecnica efficacissima, ma può una funzione richiamare se stessa?

function x()
{
    x();
}

richiamandola

x();

entreremo in un errore: Uncaught RangeError: Maximum call stack size exceeded

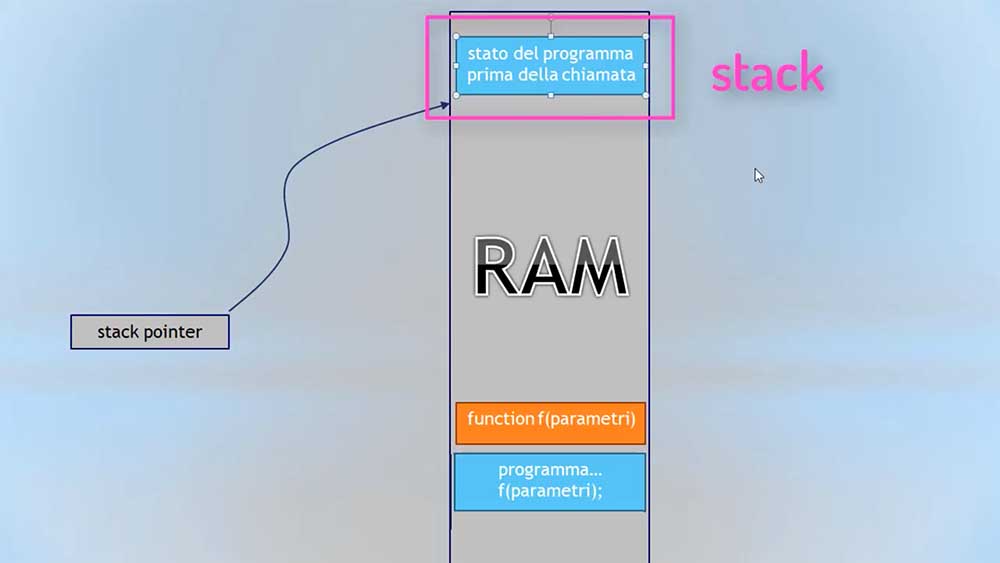
Quando il programma invoca la funzione, viene salvato sullo stack lo stato del programma. Lo stack (pila) è un’area della memoria di dimensioni variabili, riservata a memorizzare temporaneamente alcuni dati. Lo stack pointer  è come una variabile, tiene traccia del punto fino al quale lo stack sta crescendo o diminuendo. Man mano che lo stack aumenta l’indirizzo registrato nello stack pointer cambia. Trovano posto nello stack anche i parametri di una funzione, le variabili locali e anche il risultato della funzione, aumentando le dimensioni dello stack (appilati come fossero piatti). Quando viene finita l’esecuzione della funzione viene effettuato il processo inverso, svuotando la pila e si potrà continuare il contesto del programma.

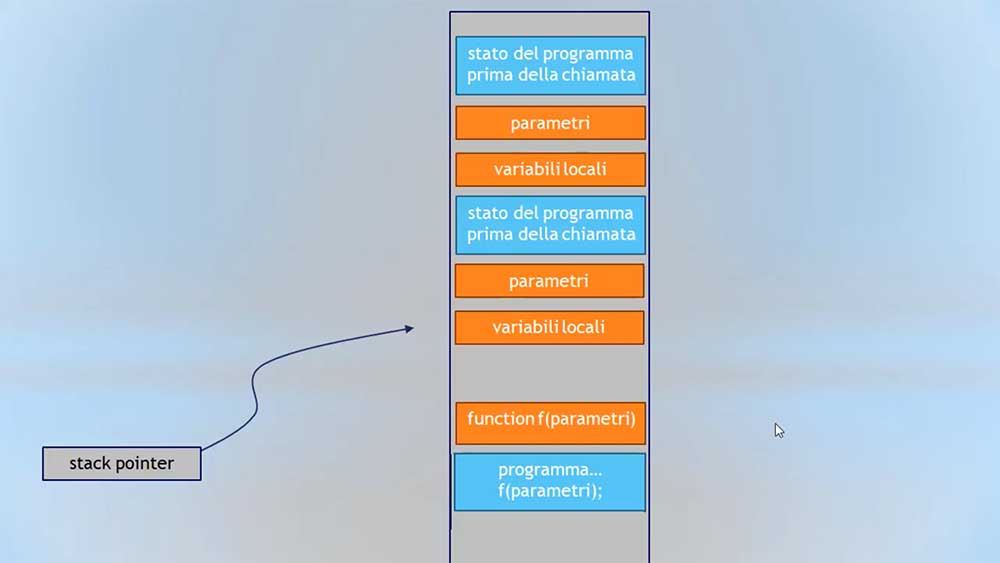
Quando una funzione ne chiama un altra, la procedura si ripete e l’incremento di spazio sulla memoria dello stack continua.

Il meccanismo che richiama una funzione impegna notevoli risorse e calcoli. Nel nostro caso la funzione f chiama f che chiama f , andremo ad esaurire lo spazio massimo per lo stack.

La domanda che viene ovvia è: perché l’interprete del linguaggio non blocca l’esecuzione di questo loop di funzione?

A questa apparente pazzia, hanno addirittura dato un nome: ricorsione, e si ha quando una funzione invoca se stessa. Sorprendentemente questa tecnica si rivela utilissima ed è alla base di moltissimi potenti algoritmi creati, basta solo recintarla, facendo in modo che la catena di loop si fermi.

//ricorsione
function x(contatore)
{
    if (contatore>10) {
        return; //base della ricorsione caso terminatore
    }
    else
    {
        x(++contatore); //passo ricorsivo
        writeln(contatore);
    }
}

x(0);

dando il valore 0 al contatore il primo if sarà false e quindi il return che terminerà la ricorsione, chiamata anche base della ricorsione, non verrà eseguito. Scatterà l’else  che eseguirà il cosiddetto passo ricorsivo ovvero la funzione richiama se stessa (x(++contatore) ); , ma lo fa con un passo diverso, in quanto lo farà avvicinare al caso terminatore ( x(1); ).

Da questo momento il flusso si blocca e viene eseguita x(1); che rifarà ricosivamente il precedente percorso, fino ad incontrare il successivo passo ricorsivo che eseguirà x(2); e così via, finché x(10) chiamerà x(11) che è maggiore di 10. A quel punto trova vera la condizione contatore>10 che farà eseguire il return. Il return non restituirà nulla, ma interromperà la funzione ricorsiva. Il valore sarà quindi passato al flusso precedente che stamperà il valore 10. La funzione x(10) che è in attesa riceverà indietro anch’essa il valore e camperà 9 … Quando arriveremo nell’ultima funzione in memoria nello stack X(0), stamperà l’ultimo valore restituito dalla precedente funzione x(1). La ricorsione, infatti stamperà una serie di numeriche da 11 decresce fino ad 1, la ricorsione infatti eseguirà con l’ordine inverso rispetto alle funzioni chiamate.

Un esempio per dimostrare la potenza delle funzioni ricorsive è il classico gioco della torre di Hanoi. Senza la ricorsione ci vorrebbero uno sproposito di righe di codice per svilupparlo, invece con poche righe eccolo risolto

function hanoi(numDischi, pioloA, pioloB, pioloC)
{

    if (numDischi>0)
    {
        hanoi(numDischi-1, pioloA, pioloC, pioloB);
        writeln("Sposta da " + pioloA + " a " + pioloB);
        hanoi(numDischi-1, pioloC, pioloB, pioloA);
    }
}

hanoi(3, "A" , "B " , "C");